等腰三角形的性质(等腰三角形三线合一)

等腰三角形的性质

等腰三角形(isoscelestriangle),是指至少有两边相等的三角形。相等的两个边称为这个三角形的腰。等腰三角形中,相等的两条边称为这个三角形的腰,另一边叫做底边。两腰的夹角叫做顶角,腰和底边的夹角叫做底角。等腰三角形的两个底角度数相等(简写成“

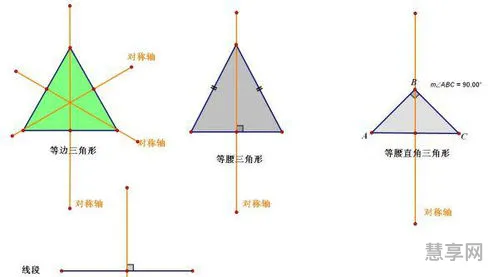
等腰三角形是轴对称图形,其对称轴是顶角平分线、底边上的中线、底边上的高所在的直线。等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。轴对称图形可以是等腰三角形、等腰直角三角形、正方形、长方形、梯形、等腰梯形、等边三角形等。

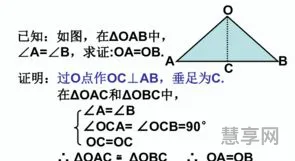
在等腰三角形中,两条底边相等,因此连接这两条底边的边(高线)垂直平分底边。根据垂直平分线定理,这条高线将底边平分成两段,并且把等腰三角形划分为两个全等的直角三角形。

等腰三角形是指至少有两边相等的三角形,相等的两个边称为这个三角形的腰。等腰三角形中,相等的两条边称为这个三角形的腰,另一边叫做底边。两腰的夹角叫做顶角,腰和底边的夹角叫做底角,等腰三角形的两个底角度数相等。

等腰三角形三线合一

如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴。(对于一个图形来说)

等腰三角形是轴对称图形,等腰三角形只有一条对称轴,等腰三角形的两个底角度数相等,两条腰长度相等,所以两边对折后可以完全重合,所以它是轴对称图形。

垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。线段垂直平分线上的点到线段两端的距离相等。

在等腰三角形中,两条底边相等,因此它们到高线的距离也相等。由于垂直平分线定理,高线将底边平分成两段,每一段的长度也相等。因此,等腰三角形的高线也相等。

由于它们被同一条高线分开,等腰三角形的两个顶角必须相等。因此,在一个等腰三角形中,两侧角和它们所对的角度也必须相等。

等腰三角形知识点总结

把一格图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称。这条直线就是对称轴。两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点。(对于两个图形来说)

11、定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边

定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似

通过学习第一章和第六章的内容,你会发现这些数学知识的奥秘并非遥不可及。相反,它们将成为你探索更高级数学主题的基础。现在就加入我们,一起揭开等腰三角形和直角三角形的神秘面纱吧!