等边三角形的定义(什么叫等边三角形)

等边三角形的定义

等边三角形可以用来衡量三角形中各个参数的值,如以等边三角形为基准,计算其他三角形的周长、面积、角度等参数。

首先,我们知道等边三角形的特征是三条边长度相等,因此我们可以通过已知的BC长度推出AB的长度为8。然后,根据等边三角形的性质,可以得出角AOB为120度,进而通过三角函数的关系式计算出角AOC、BOE等角度,最终得出DE/BE=√3/2,进而可以求出BE的长度为6/√3。最终,可以得出AB的长度为8+12=20。

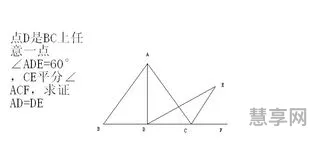
由此可见,等边三角形的应用非常广泛,是中小学数学教学中的重要内容。只要熟练掌握其特征和性质,并善于应用,就能在解决各种数学问题时得心应手。

等边三角形的性质和定义,一、等边三角形的性质和定义1、等边三角形三条边都相等的三角形叫等边三角形。其三个内角相等,均为60°,它是锐角三角形的一种。等边三角形是特殊的等腰三角形,它拥有等腰三角形的一切性质。2、等边三角形的性

在$△ABC$中,∵$∠A=∠B=∠C$,∴$△ABC$为等边三角形B.在$△ABC$中,∵$AB=AC$,且$∠B=∠C$,∴$△ABC$为等边三角形C.在$△ABC$中,∵$∠A=60°$,$∠B=60°$,∴$△ABC$为等边三角形D.在$△ABC$中,$∵AB=AC$,$∠B=60°$,∴$△ABC$为等边三角形

什么叫等边三角形

解析:$∠A=∠B=∠C$,所以$△ABC$为等边三角形,故A选项正确;$AB=AC$且$∠B=∠C$,$△ABC$不一定是等边三角形,故B选项错误;$∠A=60°$,$∠B=60°$,三个内角都是60°,所以$△ABC$为等边三角形,故C选项正确;$AB=AC$,$∠B=60°$,三个内角都是60°,所以$△ABC$为等边三角形,故D选项正确。故选B。

三角形是数学中的基础概念,也是几何学中的重要内容。它由三条线段组成,是一个三角形形状的图形。三角形具有很多性质和特点,本文将从多个角度对三角形进行分析,以便更好地理解它的概念和性质。一、根据角度分类

三角形是数学中的基础概念,有很多不同的分类方法。除了按角度、边长和形状分类外,三角形还有一些共性的性质,包括角度和为180度、两边之和大于第三边等等。这些性质和分类方法对于理解三角形的概念和性质非常重要。

4分式的加、减、乘、除、乘方的混合运算的运算顺序:先乘方、再乘除、后加减,同级运算中,谁在前先算谁,有括号的先算括号里面的,也要注意灵活,提高解题质量。

在运算过程中,要明确每一步变形的目的和依据,注意解题的格式要规范,不要随便跳步,以便查对有无错误或分析出错的原因。

证明三角形为等边三角形的条件

常见的正多边形有正三角形、正方形、正五边形、正六边形,其中它们的内角分别是60°、90°、108°、120°

若要转载原创文章用于商业用途,请联系我们,未经同意不得转载。任何转载请注明文章来源。如有问题,请联系我们,谢谢!

一个多边形任意一边向两方无限延长成为一条直线,如果多边形的其他各边均在此直线的同旁(不在直线的同旁),那么这个多边形就叫做凸多边形(凹多边形)。