什么是正三棱锥(直三棱锥定义和性质)
什么是正三棱锥
接下来,让我们进一步了解正三棱锥的特性。正三棱锥的表面积和体积是我们关注的重点之一。通过计算底面和侧面的面积,并且加上底面到顶点的距离,我们可以得到正三棱锥的表面积和体积公式。
在实际工程和测量中,正三棱锥的立体测量技术一直是一个重点和难点。通过一些新的测量技术和设备,我们可以更加精准地进行正三棱锥的立体测量,这可以帮助我们更好地应用正三棱锥的特性和性质。
在数学和几何学中,我们经常需要进行一些对正三棱锥的计算和推导。比如说,计算正三棱锥的体积和表面积,使用勾股定理和三角函数进行相关运算,以及如何利用正三棱锥的特性来解决一些数学问题等等。这些计算方法是我们学习和应用正三棱锥的重要内容。
通过这个清晰的定义,我们可以更好地理解正三棱锥的基本构造和特点。正三棱锥具有对称性,几何形状优美,是一种非常有特色的多面体。
直三棱锥定义和性质
为了更好地展示正三棱锥的立体图形和特性,我们可以通过一些计算软件和几何模型来进行展示。通过立体图形展示,我们可以更加直观地感受正三棱锥的形状和特点,这也是一种非常有效的教学和研究方法。
为了更好地理解正三棱锥的定义与特性,我们可以通过一些实际案例来进行分析。比如说,一些古代建筑中存在的正三棱锥结构,或者一些现代工程中利用正三棱锥形状设计的建筑物,都可以帮助我们更加直观地感受正三棱锥的特点和实际应用。
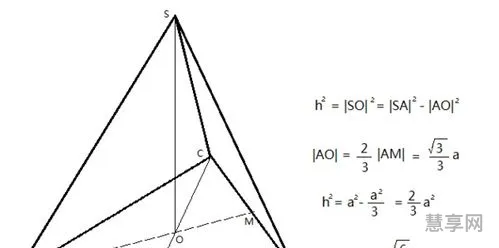
除此之外,正三棱锥还具有一些独特的性质,比如说它的高度可以用勾股定理求解,它的侧面积可以用正弦定理求解,这些性质使得正三棱锥在几何学中有着重要的地位和应用。
虽然在这篇文章中我已经为大家简要介绍了正三棱锥的定义与特性,但是正三棱锥作为一个复杂而丰富的几何图形,还有许多深入的内容值得我们进一步探讨。比如说,正三棱锥的拓展和推广,正三棱锥在不同数学问题中的应用,以及正三棱锥与其他多面体的关系等等,都是我们可以继续深入研究和讨论的内容。希望大家能够在学习和实践中不断探索,发现更多关于正三棱锥的奥秘。
正三棱锥和球的联系与区别
正三棱锥在空间中的稳定性一直是一个备受关注的问题。通过对正三棱锥的稳定性进行分析,我们可以发现,正三棱锥具有很好的稳定性,同时也可以通过一些特定的方法来加强其稳定性。比如说,在实际工程中可以通过加固材料和结构设计来提高正三棱锥的稳定性,这是一个非常值得研究和探讨的问题。
今天我想和大家一起来浅谈一下关于正三棱锥的定义与特性。正三棱锥是几何学中的一个重要概念,它具有独特的特点和性质。在接下来的文章中,我将会从不同的角度和方面来为大家详细介绍正三棱锥的定义与特性,希望能够帮助大家更深入地了解这个几何图形。
在现实生活中,正三棱锥其实有着许多的应用。比如在建筑结构中,正三棱锥的形状可以帮助我们设计和构建一些特殊的建筑物,比如一些塔楼或者尖顶建筑。在工程测量中,正三棱锥的特性也可以用来进行一些测量和计算,有着广泛的实际应用。
让我们来看一下正三棱锥的定义。正三棱锥是一种具有三个等边三角形和一个正三角形作为底面的多面体。在正三棱锥中,三个侧面都是等边三角形,底面是一个正三角形,而且从顶点到底面中心的距离与三条棱的长度相等。